How To Convert Base 10 To Base 8

Number System Conversions-

Before you go through this commodity, brand sure that y'all have gone through the previous article on Basics of Number System.

In number organisation,

• It is very important to have a proficient knowledge of how to convert numbers from one base to another base.
• Here, we volition learn how to convert any given number from base 10 to base 8.

Decimal to Octal Conversion-

A given number can exist converted from base 10 to any other base of operations using division method and multiplication method.

Following two cases are possible-

Case-01: For Numbers Carrying No Fractional Part-

• Division Method is used to catechumen such numbers from base 10 to another base.
• The division is performed with the required base.

Steps To Catechumen From Base x to Base 8-

• Divide the given number (in base x) with 8 until the consequence finally left is less than eight.
• Traverse the remainders from bottom to top to get the required number in base 8.

Case-02: For Numbers Carrying A Fractional Role-

To convert such numbers from base 10 to another base of operations, real part and fractional part are treated separately.

For Real Part-

The steps involved in converting the existent part from base 10 to another base of operations are same as above.

For Fractional Role-

• Multiplication Method is used to catechumen fractional part from base 10 to another base.
• The multiplication is performed with the required base.

Steps To Convert From Base 10 To Base of operations viii-

• Multiply the given fraction (in base of operations x) with 8.
• Write the real function and fractional part of the issue so obtained separately.
• Multiply the fractional part with 8.
• Write the existent role and partial role of the result then obtained separately.
• Echo this procedure until the partial office remains 0.
• If fractional office does non terminate to 0, find the result upward to every bit many places every bit required.

Required Number in Base 8

= Series of real part of multiplication results obtained in the above steps from top to bottom

Also Read- Conversion to Base 10

PRACTICE PROBLEMS BASED ON DECIMAL TO OCTAL CONVERSION-

Bug-

Convert the following numbers from base of operations ten to base 8-

1. (1032)_ten
2. (1032.6875)_ten
3. (172)_x
4. (172.878)₁₀

Solution-

1. (1032) ₁₀

(1032)_x → (?)₈

Using division method, we have-

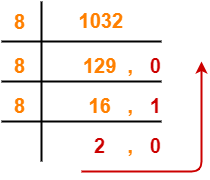
From here, (1032)₁₀ = (2010)_viii

2. (1032.6875) ₁₀

(1032.6875)₁₀ → ( ? )₈

Here, we care for the existent role and fractional part separately-

For Real Part-

• The real part is (1032)_x
• Nosotros convert the real part from base 10 to base viii using partitioning method same equally above.

So, (1032)₁₀ = (2010)₈

For Partial Function-

• The fractional part is (0.6875)₁₀
• We convert the fractional function from base 10 to base 8 using multiplication method.

Using multiplication method, nosotros have-

	Real function	Fractional Part
0.6875 x 8	5	0.5
0.5 x eight	4	0.0

Explanation

Stride-01:

• Multiply 0.6875 with 8. Event = five.v.
• Write five in existent part and 0.v in partial function.

Footstep-02:

• Multiply 0.v with eight. Result = 4.0.
• Write 4 in existent part and 0.0 in fractional part.

Since fractional part becomes 0, and so we stop.

• The fractional part terminates to 0 afterward 2 iterations.
• Traverse the real part cavalcade from top to bottom to obtain the required number in base eight.

From here, (0.6875)₁₀ = (0.54)_viii

Combining the result of real and fractional parts, we take-

(1032.6875)₁₀ = (2010.54)_viii

3. (172) ₁₀

(172)₁₀ → ( ? )_eight

Using partitioning method, we have-

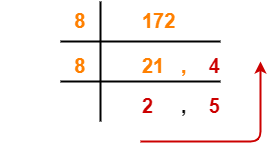
From here, (172)_x = (254)_eight

4. (172.878) ₁₀

(172.878)₁₀ → ( ? )_eight

Here, we treat the real office and fractional part separately-

For Existent Role-

• The real role is (172)₁₀
• We convert the existent part from base 10 to base 8 using sectionalisation method same every bit above.

And then, (172)_x = (254)₈

For Partial Part-

• The partial part is (0.878)_x
• We convert the fractional part from base 10 to base of operations 8 using multiplication method.

Using multiplication method, we have-

	Real part	Fractional Role
0.878 x 8	seven	0.024
0.024 x 8	0	0.192
0.192 x 8	i	0.536
0.536 x 8	4	0.288

• The fractional role does not terminates to 0 after several iterations.
• So, let united states notice the value upward to 4 decimal places.
• Traverse the existent part column from summit to bottom to obtain the required number in base 8.

From here, (0.878)₁₀ = (0.7014)₈

Combining the result of real and partial parts, we have-

(172.878)₁₀ = (254.7014)₈

As well Read- Decimal to Binary Conversion

To proceeds better agreement about Decimal to Octal Conversion,

Watch this Video Lecture

Adjacent Article- Decimal to Hexadecimal Conversion

Become more notes and other study textile of Number System.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Summary

Article Name

Decimal to Octal Conversion | Base 10 to Base 8

Description

Decimal to Octal Conversion- We use sectionalization method to convert a given decimal number to octal form. Decimal to Octal Conversion Examples. Convert the given numbers from base ten to base of operations 8.

Author

Akshay Singhal

Publisher Proper name

Gate Vidyalay

Publisher Logo

Source: https://www.gatevidyalay.com/converting-decimal-to-octal-base-10-to-base-8/

Share this post